Ratios from the Intersections of 10 + 1 Proportionalities
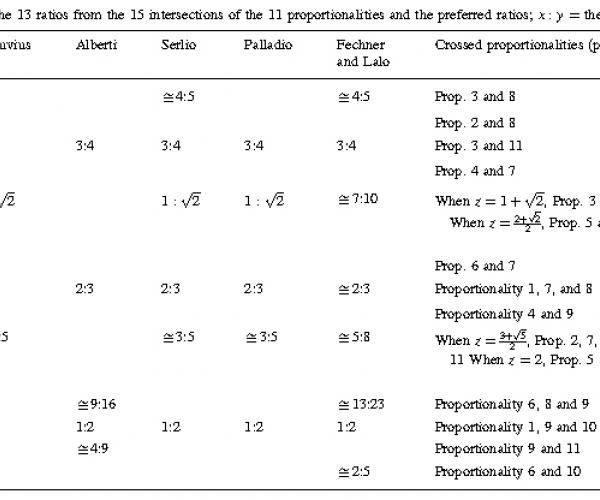
An innovative mathematical analysis comparing sets of preferred ratios from authors from antiquity (Vitruvius), the Renaissance (Alberti, Serlio and Palladio), and the modern age (Fechner and Lalo) with the eleven unique and universal
proportionalities sheds new light on architects’ use of certain ratios to endow their creations with commensurability and beauty. Some ratios may provide more ways of representing three magnitudes, and this might provide a clue to their enduring appearance in architectural works.
DESCRIPTION
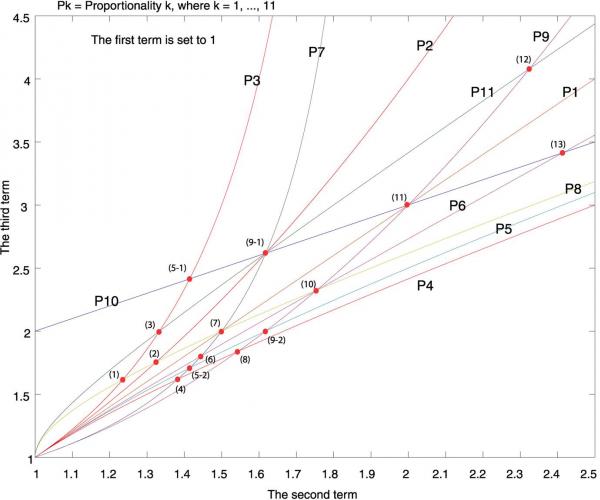
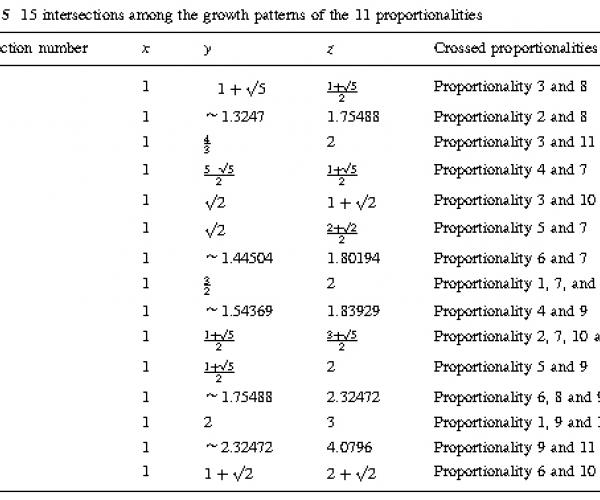
This paper shows that certain ratios between x and y provide various ways of establishing commensurability among three ordered real numbers (0\x\y\z) and their differences (z - y, y - x, z - x) when z is defined according to the 11 proportionalities. In other words, when x and y have a particular ratio, there is a higher probability that different proportionalities have the same z. This means that the particular ratios can provide more ways of representing three ordered numbers among the dimensions of an object and their differences with the equalities of the ratios among the ordered numbers. They provide a variety of commensurability for understanding or appreciating an object. This may hint at a possible underlying reason as to why certain ratios have been cherished and repeatedly employed in architecture and design throughout the ages.
Our understanding of where we live
is not so philosophical but rather pragmatic
Understanding urban environment with quantifiable measures has been the source of debates
Well then becomes the one of heated discussions … now possiblly the one of main trends